Ulam Spiral Explorer


Stanislaw Ulam, photo by the Los Alamos National Laboratory, public domain.
Before we describe the Ulam Spiral, we have to mention its discoverer, Stanislaw Ulam, one of several brilliant mathematicians associated with the development of nuclear weapons. Born into a wealthy Jewish family in Lwów, Poland, Ulam was invited to study at Princeton on the eve of Nazi ascendance in neighboring Germany by John von Neumann, another brilliant but morally ambiguous mathematician who rose to prominence during WW2 and the Cold War.

After doing significant work in ergodic theory and becoming an American citizen, the outbreak of the Second World War and his friendship with von Neumann led to his joining the Manhattan Project which developed the first nuclear weapons. After the war, he continued working at Los Alamos with Edward Teller and Enrico Fermi to develop the Teller-Ulam design, the basis of all subsequent thermonuclear bombs.

When he wasn't busy directly laying the groundwork for the extinction of the human race, he did important on potential means of interstellar travel (using nuclear explosions for propulsion), nonlinear science, group theory, combinatorics, projective algebra, topology, and several other branches of mathematics, and the crucially important Monte Carlo method, so useful to both computational physics and—ahem—the continued development of nuclear weapons, was his brainchild.

One day in 1963, while bored with a presentation during a scientific conference, he idly doodled the spiral that would come to bear his name.

The Ulam Spiral

Ulam's doodle consisted of the positive integers, starting with 1, arranged in a counter-clockwise spiral in a grid.

Circling all of the prime numbers, he noticed that the primes fell along semi-regular diagonals.

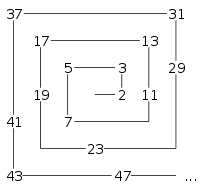
Extending this to a larger spiral, the diagonals are much more obvious. In the rendering of a 200&mult;200 spiral below, the primes form a distinct fabric-like pattern, which leads to the spiral's name in many other languages, the Ulam Cloth.

The Ulam Spiral Explorer

I started working on the Ulam Spiral Explorer (which is still very much a work in progress) because the semi-regularity of the "cloth" reminded me a great deal of something I used to see back during the 8-bit era on my Apple //e. This was way before there were much in the way of standardized image file formats, so if you wished to save the contents of the screen, you simply copied video memory directly to a file. To view the image, you had to load it back into memory at the original address, which had to be specified as part of the BLOAD command.

Naturally, it was easy to get the memory address wrong through a simple typo. Since such typos were most often a single wrong or transposed digit, the image data was often loaded at a position a little before or a little after the start of video memory. This resulted in a characteristic skewed appearance where pixels that should have been atop each other were offset by the difference between the beginning of video RAM and the actual address the data had been copied to.

The appearance of structured data, i.e., an actual image of some kind, being skewed in this way is very different from truly random data.

So I wrote the Explorer initially to test my hypothesis that tweaking the parameters of the spiral, chiefly the aspect ratio and the starting point, would reveal the "correct" dimensions when the semi-regular diagonals suddenly snapped into being fully regular diagonals.

While my experiments in that direction have been less than exhaustive, that magic moment never occurred, and I no longer think the original hypothesis is valid. Or rather, I no longer think the shape of integer space is a two-dimensional rectilinear grid. Other shapes remain unexplored (but see Earlier Work and Variations below).

Nevertheless, work on the current version of the Explorer continues, some of which is serious, mathematical experimentation, and a lot of which is purely aesthetic, using the Ulam Spiral as the basis of abstract art. In both cases, you are welcome to use the Explorer to pursue explorations of your own.

Earlier Work and Variations

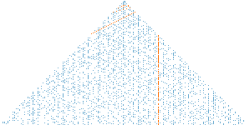
Ulam was not the first person to notice some regularity in the distribution of the primes through geometric methods. In 1932, the herpetologist Lawrence Klauber presented a triangular, non-spiral matrix to the American Mathematical Society which demonstrated similar patterns. Perhaps unsurprisingly, the lines of primes in the Klauber triangle meet at 60° angles instead the 90° angles in the Ulam Spiral.

Seven years before Ulam's discovery, Arthur C. Clarke described the spiral in his novel The City and the Stars but apparently did not actually construct the spiral and thus failed to notice the patterns.

In 1994, Robert Sacks discovered another semi-regular spiral arrangement of the integers by plotting them along an Archimedean spiral, suggesting that it is the spiral that is essential, not the grid.

Future work in this area, time permitting, will add the Klauber Triangle and the Sacks Spiral to the Explorer.

Other Resources

As is often the case with mathematical topics, the Wikipedia article on the spiral is a good starting point for further exploration.

It should probably come as no surprise that I'm not the first or only person to use software to investigate the Ulam Spiral. H. Rudd has an entire site devoted to it, including a free downloadable desktop implementation, complete with links to even more goodies.

Credits and Licensing

Excluding output from the Ulam Spiral Explorer itself, the images on this page were taken from the Wikipedia article on the Ulam Spiral, which are shared under an open license. In particular:

The Ulam Spiral Explorer is free to use and modify under the BSD license.